 #1
Non ho ben capito perché si possa dire che in un legame
ingresso-uscita in cui compaiono termini fino alla derivata seconda
dell'uscita e solo fino alla derivata prima dell'ingresso, l'assenza
della derivata seconda dell'ingresso permetta di evincere che il sistema
risulta puramente dinamico. Mi riferisco al terzo test del primo capitolo
sul testo Teoria dei Sistemi: Test commentati e risolti.
(Mirko Tedaldi)
#1
Non ho ben capito perché si possa dire che in un legame
ingresso-uscita in cui compaiono termini fino alla derivata seconda
dell'uscita e solo fino alla derivata prima dell'ingresso, l'assenza
della derivata seconda dell'ingresso permetta di evincere che il sistema
risulta puramente dinamico. Mi riferisco al terzo test del primo capitolo
sul testo Teoria dei Sistemi: Test commentati e risolti.
(Mirko Tedaldi)
 La condizione (che viene data nella discussione della domanda) può
venire dimostrata facendo riferimento alla soluzione della equazione
differenziale che costituisce il modello del sistema considerato.
Una via parallela di buona efficacia mnemonica consiste nel fare riferimento
ai modelli a tempo discreto; l'esempio considerato avrebbe un modello del
tipo y(t+2)+3y(t+1)y(t)+ 2y(t)=u(t)+u(t+1) che risulta, ovviamente,
puramente dinamico.
La condizione (che viene data nella discussione della domanda) può
venire dimostrata facendo riferimento alla soluzione della equazione
differenziale che costituisce il modello del sistema considerato.
Una via parallela di buona efficacia mnemonica consiste nel fare riferimento
ai modelli a tempo discreto; l'esempio considerato avrebbe un modello del
tipo y(t+2)+3y(t+1)y(t)+ 2y(t)=u(t)+u(t+1) che risulta, ovviamente,
puramente dinamico.
 #2
Mi sembra di avere capito che a volte risposta e uscita vengano usate in
modo intercambiabile. È corretto? (Daniele Cremonini)
#2
Mi sembra di avere capito che a volte risposta e uscita vengano usate in
modo intercambiabile. È corretto? (Daniele Cremonini)
 Con il termine uscita si indica una parte degli attributi misurabili
di un sistema dinamico orientato. Il termine può venire usato per indicare
tali attributi in un istante specifico, in un intervallo di tempo assegnato
o in un intervallo di tempo generico; l'interpretazione corretta dipende
dal contesto nel quale il termine viene usato.
Con risposta si indica sempre l'andamento dell'uscita in un intervallo
di tempo.
Con il termine uscita si indica una parte degli attributi misurabili
di un sistema dinamico orientato. Il termine può venire usato per indicare
tali attributi in un istante specifico, in un intervallo di tempo assegnato
o in un intervallo di tempo generico; l'interpretazione corretta dipende
dal contesto nel quale il termine viene usato.
Con risposta si indica sempre l'andamento dell'uscita in un intervallo
di tempo.
 #3
Qual'è la definizione di linea di trasmissione a parametri
distribuiti? (Gabriele Tinti)
#3
Qual'è la definizione di linea di trasmissione a parametri
distribuiti? (Gabriele Tinti)
 Dal punto di vista matematico, un sistema a parametri distribuiti è
un sistema il cui stato non appartiene ad uno spazio vettoriale a dimensioni
finite; la descrizione di tali sistemi richiede l'uso di equazioni
differenziali alle derivate parziali. Ciò avviene, come abbiamo
visto, nel caso delle linee di trasmissione reali, caratterizzate da
capacità e induttanze distribuite lungo la linea ed avviene
pure per la maggior parte dei sistemi fisici reali. Nella pratica
è frequente l'uso di modelli a parametri concentrati anche per
sistemi a parametri distribuiti poiché tali modelli risultano
di più agevole utilizzazione; la scelta dell'ordine
determina, in questi casi, l'approssimazione con la quale il modello
descrive il processo reale.
Dal punto di vista matematico, un sistema a parametri distribuiti è
un sistema il cui stato non appartiene ad uno spazio vettoriale a dimensioni
finite; la descrizione di tali sistemi richiede l'uso di equazioni
differenziali alle derivate parziali. Ciò avviene, come abbiamo
visto, nel caso delle linee di trasmissione reali, caratterizzate da
capacità e induttanze distribuite lungo la linea ed avviene
pure per la maggior parte dei sistemi fisici reali. Nella pratica
è frequente l'uso di modelli a parametri concentrati anche per
sistemi a parametri distribuiti poiché tali modelli risultano
di più agevole utilizzazione; la scelta dell'ordine
determina, in questi casi, l'approssimazione con la quale il modello
descrive il processo reale.
 #4
È corretto affermare che due sistemi in parallelo non costituiscono
mai un sistema completamente raggiungibile, anche se i due sistemi
interconnessi sono completamente raggiungibili? (Mirko Tedaldi)
#4
È corretto affermare che due sistemi in parallelo non costituiscono
mai un sistema completamente raggiungibile, anche se i due sistemi
interconnessi sono completamente raggiungibili? (Mirko Tedaldi)
 La connessione in parallelo di due sistemi dinamici costituisce (ovviamente)
un sistema non completamente raggiungibile quando uno dei due sistemi (o
entrambi) non godono di questa proprietà. Nel caso in cui i due
sistemi risultino entrambi completamente raggiungibili, la loro connessione
in parallelo può risultare o meno completamente raggiungibile.
La connessione in parallelo di due sistemi dinamici costituisce (ovviamente)
un sistema non completamente raggiungibile quando uno dei due sistemi (o
entrambi) non godono di questa proprietà. Nel caso in cui i due
sistemi risultino entrambi completamente raggiungibili, la loro connessione
in parallelo può risultare o meno completamente raggiungibile.
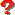 #5
Perché E-(t0,t1,u(.),y(.))
può contenere più di un elemento anche per sistemi in forma
minima? (Gabriele Tinti)
#5
Perché E-(t0,t1,u(.),y(.))
può contenere più di un elemento anche per sistemi in forma
minima? (Gabriele Tinti)
 Il sottoinsieme in oggetto può benissimo contenere più
elementi per sistemi dinamici generici e in forma minima; la definizione
di forma minima implica infatti l'assenza, nell'insieme degli stati,
di stati equivalenti. La non equivalenza tra due stati implica poi solo che
esista almeno una funzione (sequenza) di ingresso che renda possibile
distinguere tali stati, non che tale proprietà valga per ogni
funzione di ingresso; può facilmente verficare quanto sopra
facendo riferimento ai sistemi a stati finiti ed al problema della diagnosi.
Il discorso è ovviamente diverso per i sistemi lineari nei quali
la possibilità di distinguere due stati non è legata alla
applicazione di ingressi particolari.
Il sottoinsieme in oggetto può benissimo contenere più
elementi per sistemi dinamici generici e in forma minima; la definizione
di forma minima implica infatti l'assenza, nell'insieme degli stati,
di stati equivalenti. La non equivalenza tra due stati implica poi solo che
esista almeno una funzione (sequenza) di ingresso che renda possibile
distinguere tali stati, non che tale proprietà valga per ogni
funzione di ingresso; può facilmente verficare quanto sopra
facendo riferimento ai sistemi a stati finiti ed al problema della diagnosi.
Il discorso è ovviamente diverso per i sistemi lineari nei quali
la possibilità di distinguere due stati non è legata alla
applicazione di ingressi particolari.
 #6
Ho qualche problema quando mi si chiede di analizzare la memoria
di un sistema dinamico, come si deve procedere? (Gabriele Tinti)
#6
Ho qualche problema quando mi si chiede di analizzare la memoria
di un sistema dinamico, come si deve procedere? (Gabriele Tinti)
 La memoria di un sistema dinamico a tempo discreto è pari al
numero massimo di campioni di ingresso e di uscita precedenti
necessari per calcolare l'uscita del sistema in un istante generico.
La memoria di un sistema dinamico a tempo discreto è pari al
numero massimo di campioni di ingresso e di uscita precedenti
necessari per calcolare l'uscita del sistema in un istante generico.
 #7
Che cosa hanno in comune e che cosa diversifica l'osservabilità e
la diagnosticabilità? (Vittorio Teglia)
#7
Che cosa hanno in comune e che cosa diversifica l'osservabilità e
la diagnosticabilità? (Vittorio Teglia)
 La diagnosi e l'osservazione dello stato iniziale differiscono in un solo
aspetto; nell'osservazione dello stato iniziale l'ingresso si considera
assegnato, mentre nella diagnosi deve venire progettato in funzione di
tale osservazione. La completa osservabilità di un sistema
in un intervallo di tempo implica quindi sempre anche la
diagnosticabilità in tale intervallo mentre non vale, ovviamente,
la proprietà inversa.
La diagnosi e l'osservazione dello stato iniziale differiscono in un solo
aspetto; nell'osservazione dello stato iniziale l'ingresso si considera
assegnato, mentre nella diagnosi deve venire progettato in funzione di
tale osservazione. La completa osservabilità di un sistema
in un intervallo di tempo implica quindi sempre anche la
diagnosticabilità in tale intervallo mentre non vale, ovviamente,
la proprietà inversa.
 #8
Durante una lezione, lei ha posto la seguente domanda: "Come faccio a
controllare che il problema dell'osservazione dello stato iniziale abbia
soluzione?".
Non mi è chiara la risposta che, nella stessa lezione, lei ha fornito.
(Marcello Romani)
#8
Durante una lezione, lei ha posto la seguente domanda: "Come faccio a
controllare che il problema dell'osservazione dello stato iniziale abbia
soluzione?".
Non mi è chiara la risposta che, nella stessa lezione, lei ha fornito.
(Marcello Romani)
 È sufficiente verificare che l'insieme degli stati iniziali
compatibili con l'ingresso e l'uscita osservati, cioè
E-(t0,t1,u(.),y(.))
contenga un solo elemento.
È sufficiente verificare che l'insieme degli stati iniziali
compatibili con l'ingresso e l'uscita osservati, cioè
E-(t0,t1,u(.),y(.))
contenga un solo elemento.
 #9
E' giusta l'implicazione: Forma minima => Sistema diagnosticabile?
Ho pensato che se un sistema è in forma minima allora non ha stati equivalenti, se non ha stati equivalenti
esiste una funzione di ingresso u() tale che mi permette di distinguere l'uscita dalle altre possibili.
Se prendo questa funzione d'ingresso con la corrispondente uscita e ne calcolo E-(t,t0,u(),y()), questo
conterrà solo un elemento, visto che se ne contenesse di più, tali stati sarebbero equivalenti contro l'ipotesi
che il sistema fosse in forma minima? (Simone Melchiori, Mon Dec 27 17:53:26)
#9
E' giusta l'implicazione: Forma minima => Sistema diagnosticabile?
Ho pensato che se un sistema è in forma minima allora non ha stati equivalenti, se non ha stati equivalenti
esiste una funzione di ingresso u() tale che mi permette di distinguere l'uscita dalle altre possibili.
Se prendo questa funzione d'ingresso con la corrispondente uscita e ne calcolo E-(t,t0,u(),y()), questo
conterrà solo un elemento, visto che se ne contenesse di più, tali stati sarebbero equivalenti contro l'ipotesi
che il sistema fosse in forma minima? (Simone Melchiori, Mon Dec 27 17:53:26)
 Il fatto che un sistema sia in forma minima, cioè non abbia stati equivalenti, implica, in generale, che
nessuna coppia di stati generi la stessa uscita con ogni funzione di ingresso, mentre questo può
benissimo avvenire in corrispondenza ad una funzione di ingresso specifica. Naturalmente stiamo parlando,
dato che lei non specifica alcuna classe particolare, di sistemi dinamici del tutto generici; il discorso
sarebbe diverso per classi particolari, es. per i sistemi lineari.
In definitiva, un sistema può benissimo essere in forma minima senza che esista alcuna funzione di ingresso
in grado di consentire la diagnosi; questo diventa invece possibile con esperimenti multipli (riveda quanto
abbiamo detto per la diagnosi dei sistemi a stati finiti).
Il fatto che un sistema sia in forma minima, cioè non abbia stati equivalenti, implica, in generale, che
nessuna coppia di stati generi la stessa uscita con ogni funzione di ingresso, mentre questo può
benissimo avvenire in corrispondenza ad una funzione di ingresso specifica. Naturalmente stiamo parlando,
dato che lei non specifica alcuna classe particolare, di sistemi dinamici del tutto generici; il discorso
sarebbe diverso per classi particolari, es. per i sistemi lineari.
In definitiva, un sistema può benissimo essere in forma minima senza che esista alcuna funzione di ingresso
in grado di consentire la diagnosi; questo diventa invece possibile con esperimenti multipli (riveda quanto
abbiamo detto per la diagnosi dei sistemi a stati finiti).
 #10
A lezione è stato detto che un sistema è equivalente alla sua forma minima, cioè alla
sua sola parte osservabile. Due sistemi per essere equivalenti devono essere compatibili:
in genere però la parte osservabile del sistema può avere meno ingressi del sistema
complessivo e quindi potrebbero non essere compatibili. I due concetti possono comunque
essere conciliabili o il termine equivalenti è usato con un significato più ampio?
(Alessandro Caselli, Sun Jan 2 23:07:54 2000)
#10
A lezione è stato detto che un sistema è equivalente alla sua forma minima, cioè alla
sua sola parte osservabile. Due sistemi per essere equivalenti devono essere compatibili:
in genere però la parte osservabile del sistema può avere meno ingressi del sistema
complessivo e quindi potrebbero non essere compatibili. I due concetti possono comunque
essere conciliabili o il termine equivalenti è usato con un significato più ampio?
(Alessandro Caselli, Sun Jan 2 23:07:54 2000)
 La definizione data richiede, sul piano formale, l'eguaglianza del numero di ingressi
per potere definire equivalenti due sistemi e questo vale per un sistema e la sua
forma minima anche se alcuni ingressi non dovessero agire su tale parte.
Su un piano pratico si potrebbero trascurare gli ingressi che non agiscono sull'uscita
ed estendere, come lei implicitamente propone, la definizione di equivalenza a sistemi
caratterizzati da un numero diverso di ingressi; si tratta però di una questione
essenzialmente formale.
La definizione data richiede, sul piano formale, l'eguaglianza del numero di ingressi
per potere definire equivalenti due sistemi e questo vale per un sistema e la sua
forma minima anche se alcuni ingressi non dovessero agire su tale parte.
Su un piano pratico si potrebbero trascurare gli ingressi che non agiscono sull'uscita
ed estendere, come lei implicitamente propone, la definizione di equivalenza a sistemi
caratterizzati da un numero diverso di ingressi; si tratta però di una questione
essenzialmente formale.